Top 100 Liked on Leetcode 🚧
Top coding questions from Top 100 Liked on Leetcode
The list contains all the top 100 liked problems on leetcode, but the explanation is not available for all of them, just the ones which do not popup into head just by looking into them or which might be useful for you.
Letter Combinations of a Phone Number
public List<String> letterCombinationsBackTrack(String digits);
Remove Nth Node From End of List
public ListNode removeNthFromEnd(ListNode head, int n);
Find First and Last Position of Element in Sorted Array
public int[] searchRange(int[] nums, int target);
Longest Substring Without Repeating Characters
Given a string s, find the length of the longest substring without repeating characters.
public int lengthOfLongestSubstring(String s);Input: s = "abcabcbb"Output: 3 ("abc")The idea behind solving the problem is very simple, we need to keep track of the characters we have seen so far and the length of the substring.
The same can be achieved with usage of Set and a pointer to keep track of the start of the substring, and along with that we can use sliding window method to check the current length of the longest substring.
Median of two Sorted Arrays
Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
public double findMedianSortedArrays(int[] nums1, int[] nums2);Main idea behind finding the median for a 1D array is that you keep on removing the min and the max element from the array until you are either left with 1 or two elements in the array. You can apply the same concept here with using four pointers to keep track of the start end for both the sorted array.
Longest Palindromic Substring
Given a string s, return the longest palindromic substring in s.
public String longestPalindrome(String s);
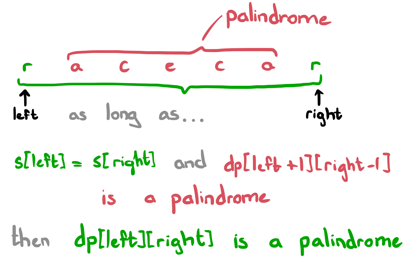
The DP approach to this question is quite simple actually! For any given substring, we can confirm if it is a palindrome in O(1) time if:
The characters at the ends of the substring are the same.
If the inner substring is a palindrome.
Which will be represented by dp[i][j] = dp[i+1][j-1] && s.charAt(i) == s.charAt(j). So the dp matrix you can imagine will look like all the true value in the diagonal center as it denotes the palindrome of a single character and all the down cells to this diagonal will be false because they represent the particular length in reverse order which we don't want.
Like wise we will be calculating the values for the top of diagonal section of the matrix. And there for every cell we would need the left-down diagonal value to be calculated first which is represented by dp[i+1][j-1].
Container With Most Water
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
public ListNode addTwoNumbers(ListNode l1, ListNode l2);
Input: height = [1,8,6,2,5,4,8,3,7] Output: 49
The idea is to maximize the distance between the two bars and for that we can take two pointers start and end. We will calculate the area by taking the minimum of the two heights and multiply it with the difference between the two pointers.
And for moving the pointers we will check wether the value at the start is less or higher that the value at the end index.
Rotate Image
You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
public void rotate(int[][] matrix);
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]
If you know some about Math, then we know that the Rotation is actually a process which is combination of Transpose and Reverse the Matrix. So Transposing means we swap the value diagonally and Reverse the matrix means we reverse the rows assuming each row as 1D Matrix.
Jump Game II
Given an array of non-negative integers nums, you are initially positioned at the first index of the array.Each element in the array represents your maximum jump length at that position.Your goal is to reach the last index in the minimum number of jumps.
You can assume that you can always reach the last index.
public int jump(int[] A);
One quick solution for the problem is that stand at the end position and check if you can reach the current position from left, meaning Find the leftmost position that can reach the current position.
public int jump(int[] nums) {
int position = nums.length - 1;
int steps = 0;
while (position != 0) {
for (int i = 0; i < position; i++) {
if (nums[i] >= position - i) {
position = i;
steps++;
break;
}
}
}
return steps;
}
TC: O(n) But for the worst case we can have a O(n^2).
To avoid that we can add an extra check at the start like below.
if len(set(nums)) < 2:
return math.ceil((len(nums)-1)/(nums[0])) if nums and nums[0] else 0
SC: O(1) but will take O(n) if we are checking for the second part.
Longest Valid Parentheses
Given a string containing just the characters '(' and ')', find the length of the longest valid (well-formed) parentheses substring.
public int longestValidParentheses(String s);
Input: s = "(()" Output: 2
The idea is to traverse the string from left to right and keep track of the number of opening and closing parentheses. If open==close then we know that this is the valid sequence and if they are not equal then we reinitialize the count of both open and close to 0. Likewise repeat the process by iterating the string from right to left.
Solution - Twice Iteration
class Solution { public int longestValidParentheses(String s) { int max=0; int open = 0, close=0; for(int i=0;i<s.length();i++){ if(s.charAt(i) == '(') open++; else close++; if(open == close){ max = Math.max(max, open*2); }else if(close>open){ open = close = 0; } } open = close=0; for(int i=s.length()-1;i>=0;i--){ if(s.charAt(i) == '(') open++; else close++; if(open == close){ max = Math.max(max, open*2); }else if(close<open){ open = close = 0; } } return max; }}TC: O(n)SC: O(1)Using stack also we can solve the problem. We keep track of checking whether the string scanned so far is a valid one and also the length of the longest valid string. In order to do so, we start by pushing -1 onto the stack. For every '(' encountered, we push its index onto the stack.
For every ')' encountered, we pop the topmost element. Then, the length of the currently encountered valid string of parentheses will be the difference between the current element's index and the top element of the stack.
Solution - Stack
class Solution { public int longestValidParentheses(String s) { int max=0; int open = 0, close=0; for(int i=0;i<s.length();i++){ if(s.charAt(i) == '(') open++; else close++; if(open == close){ max = Math.max(max, open*2); }else if(close>open){ open = close = 0; } } open = close=0; for(int i=s.length()-1;i>=0;i--){ if(s.charAt(i) == '(') open++; else close++; if(open == close){ max = Math.max(max, open*2); }else if(close<open){ open = close = 0; } } return max; }}TC: O(n)SC: O(n) As we are using Stack for the storage.